• 서론 •

지난번 게시글에서는 요트 다이스 최적 선택 알고리즘을 구현한 방법을 소개하며, 평균 점수 200점대 초반이라는 준수한 성능을 보였다고 언급했었다. 게임 플레이 에이전트를 만들었으니, 통계와 분석을 진행해 보는 것이 당연한 수순이다. 이번에는 평균 점수뿐만 아니라 다양한 데이터를 추출하여 시각화해 보았다.

• 점수 분포 살펴보기 •

최종 점수 분포

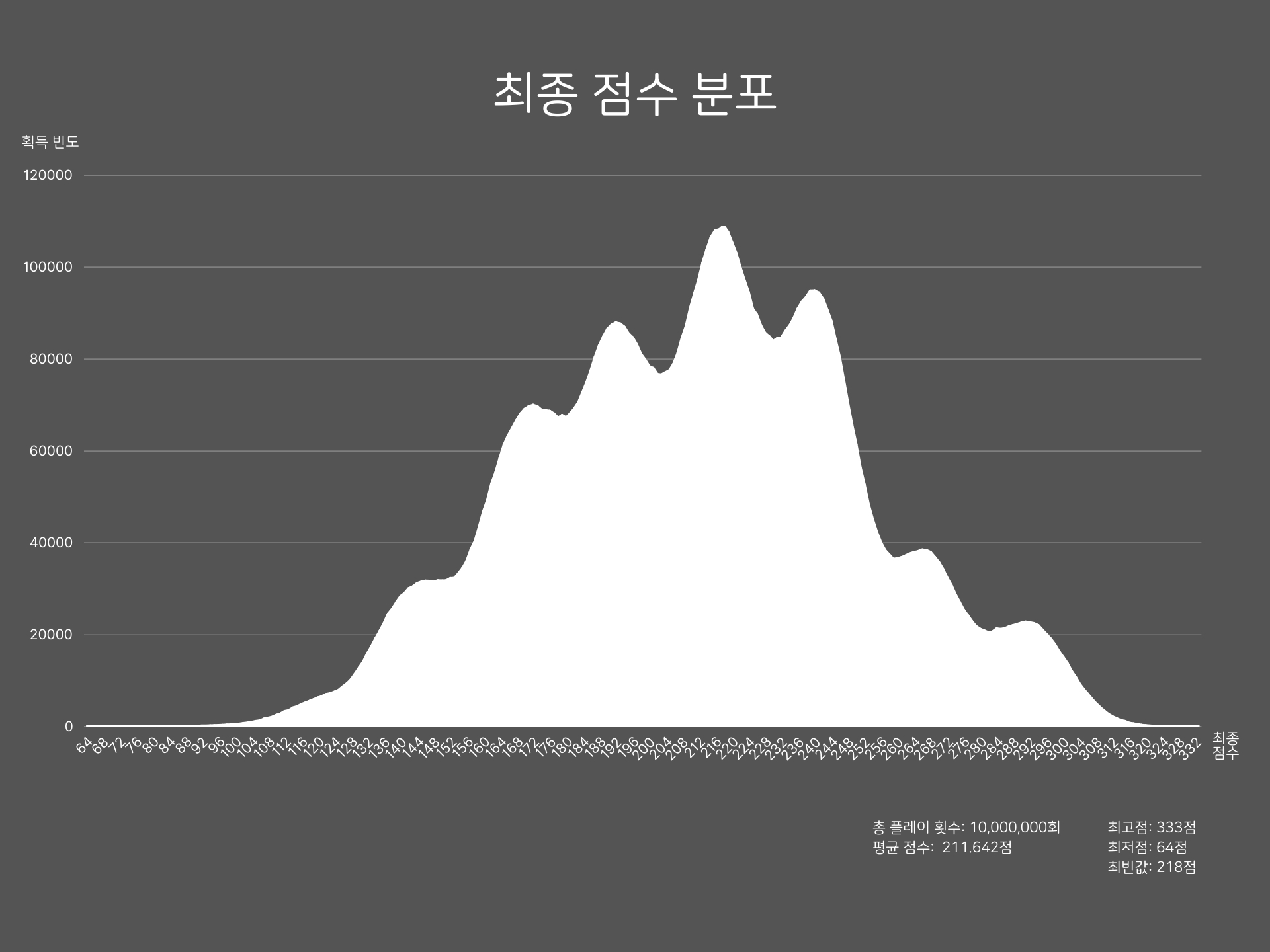
위 그래프는 천만 회의 시뮬레이션을 통해 얻은 최종 점수 분포를 나타낸다. X축은 최종 점수, Y축은 해당 점수가 나온 횟수이다.
최저점은 64점, 최고점은 333점으로 꽤 넓은 범위를 보이지만, 양쪽 극단 영역의 빈도는 매우 낮다. 따라서 매우 높은 확률로 130점에서 300점 사이의 점수를 받았다는 걸 알 수 있다.
요트 다이스에는 조건 만족 여부에 따라 점수를 얻거나 일정한 고정 점수를 획득하는 카테고리가 많아 정규 분포를 따르지 않으리란 것은 예상했지만 봉우리가 8개나 되는 올록볼록한 그래프의 형태는 예상치 못했다. 이러한 분포가 나타난 원인은 아래에서 자세히 살펴보겠다.

Aces~Sixes의 합 분포

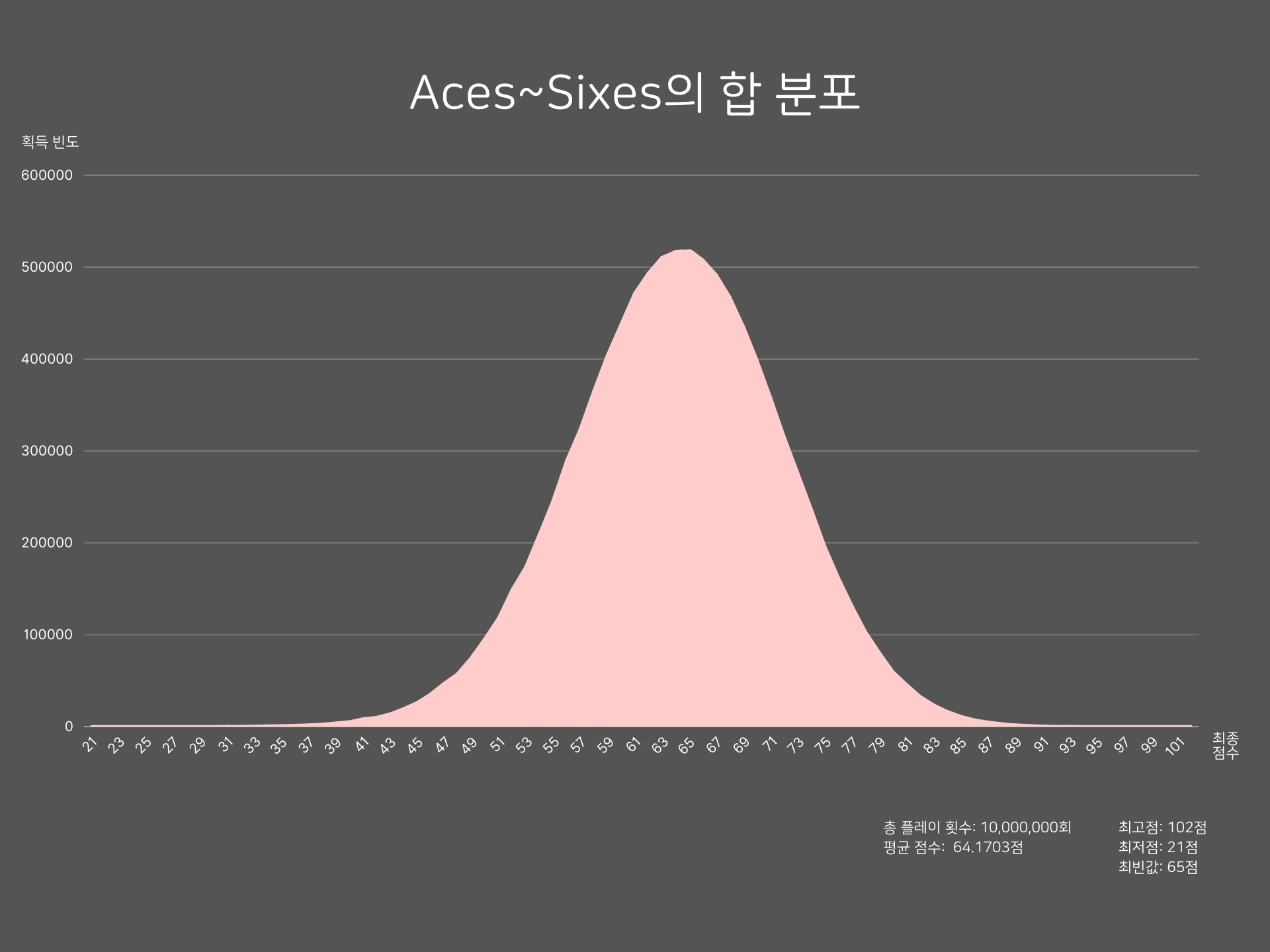
상단부 카테고리(Aces~Sixes)의 점수 합만 분리해서 그린 그래프이다. 이 부분에는 고정 점수나 특정 조건으로 점수를 얻는 카테고리가 없기 때문에, 평균 근처에 집중된 단봉형 분포가 나타났다.

Choice~Yacht의 합 분포

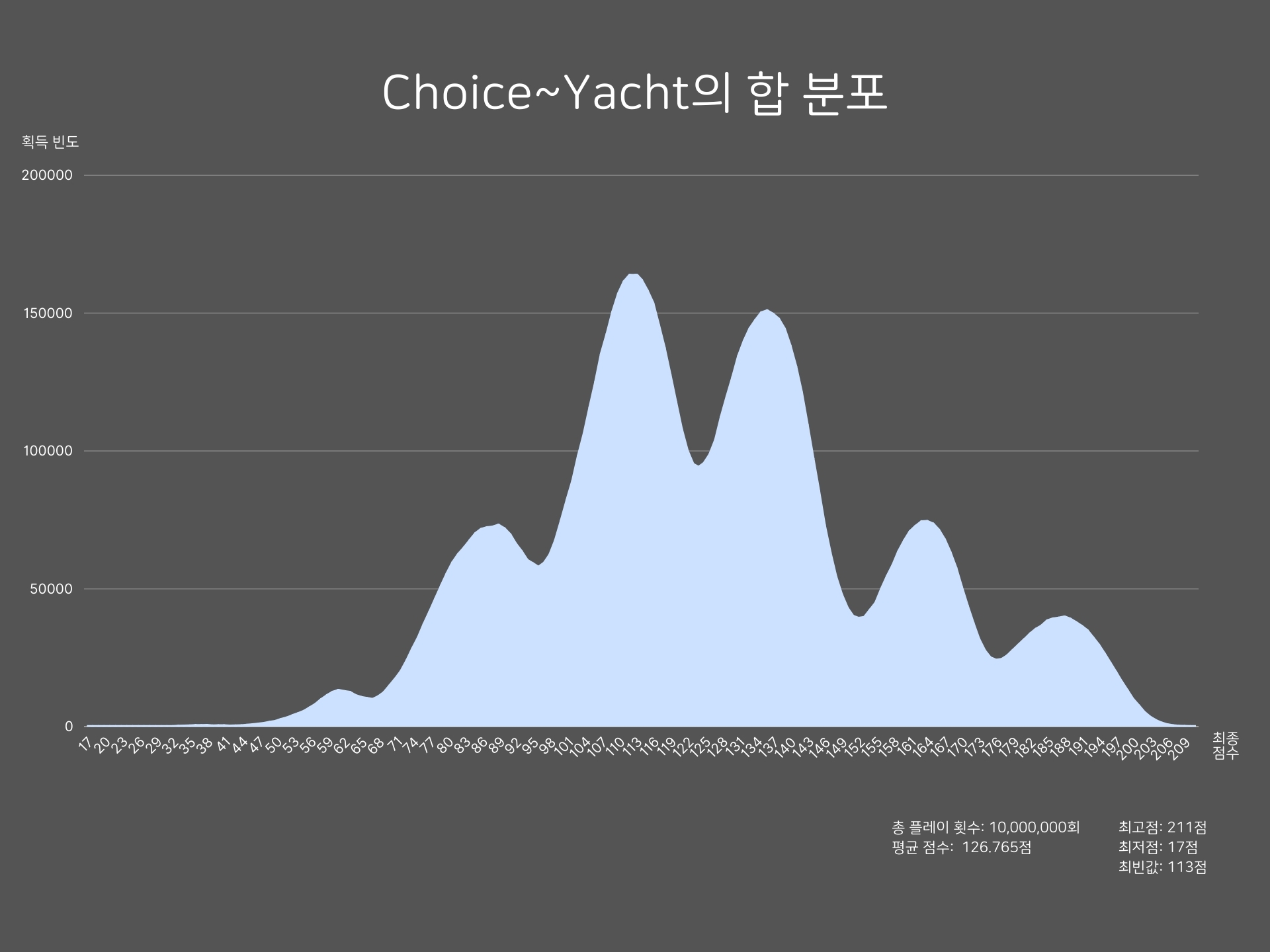
하단부(Choice~Yacht) 카테고리의 점수 합을 분리해서 그래프를 그려보니, 이 하단부가 올록볼록한 최종 점수 그래프 형태를 만들게 된 주된 원인임을 알게 되었다. 다만 이 그래프에는 봉우리가 6개만 보이는데, 최종 점수 분포에는 봉우리가 8개 나타난 이유를 아래에서 알아보자.

• 점수 분포 그래프 분석 •

용의자 1: 보너스 점수

첫 번째로, 상단부 점수가 63점 이상일 때 추가로 부여되는 보너스 점수 35점이 그래프 형태에 큰 영향을 줄 것으로 예상했다.

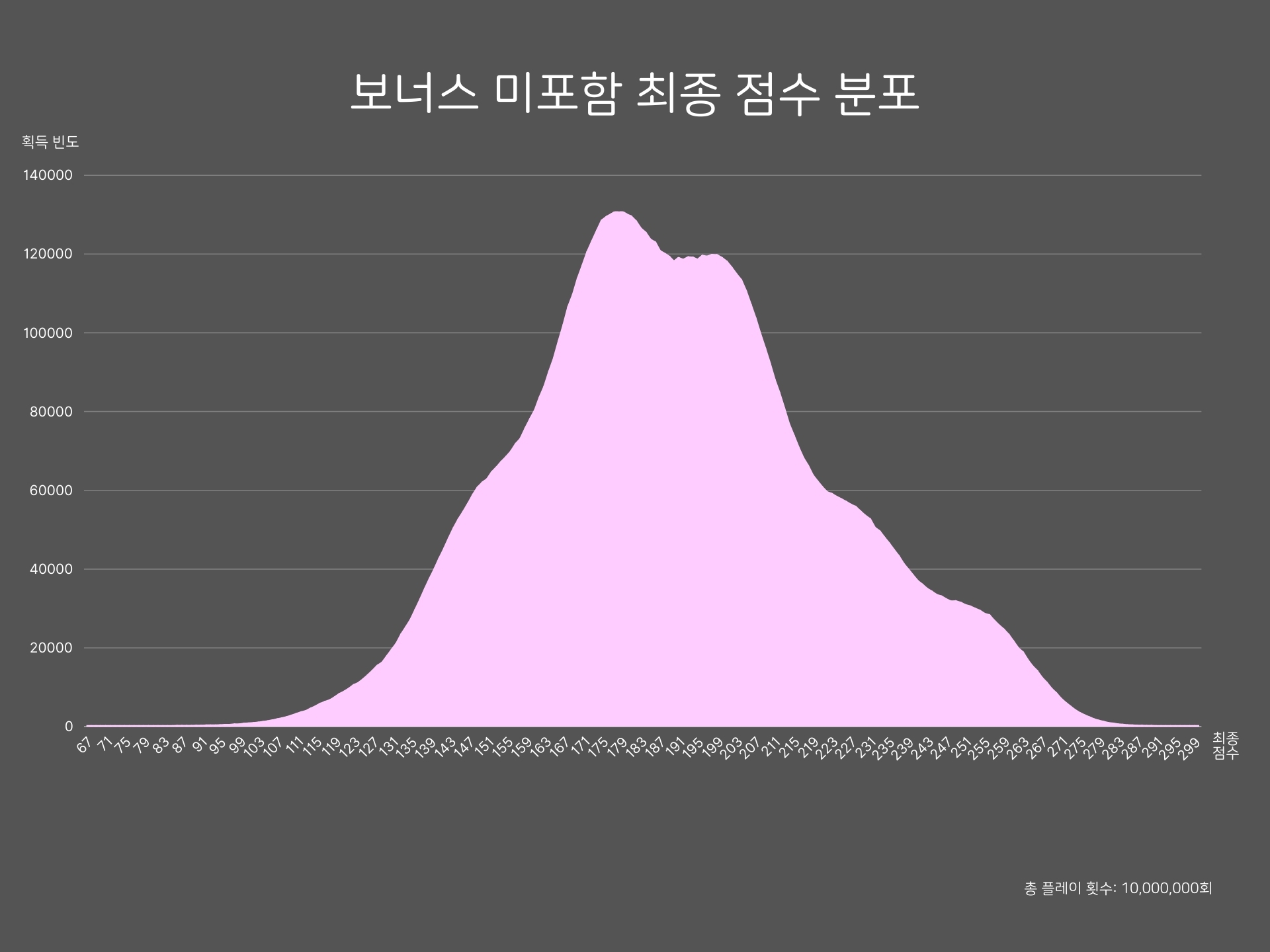
위 그래프는 최종 점수를 계산할 때, 보너스를 더해주지 않은 버전이다. 보너스가 포함된 기존 그래프보다 봉우리가 뭉툭해진 모습이 관찰된다.

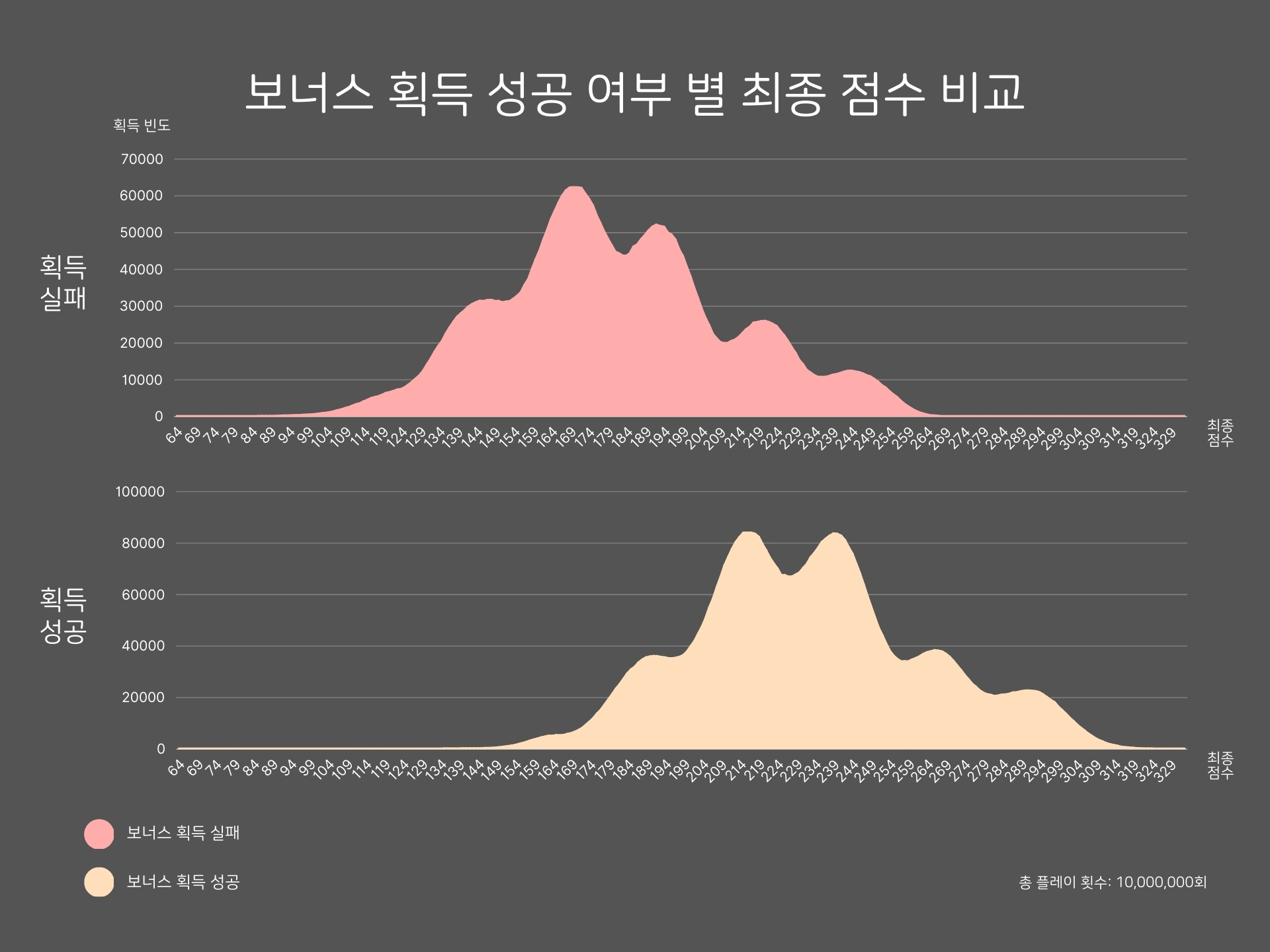
그 이유를 알기 위해 보너스를 획득에 성공한 경우와 실패한 경우를 분리해서 그래프를 그려보았다. 각 그래프에는 봉우리가 6개씩 나타나며, 두 그래프가 합쳐지면서 최종적으로 8개의 봉우리가 생겼다는 사실을 알 수 있다.

더 명확히 하기 위해 두 그래프를 누적해서 그려보았다. 위쪽 그래프는 보너스를 포함한 버전으로, 최종 점수 그래프와 동일한 모습을 볼 수 있다. 아래쪽 그래프는 보너스를 제외한 버전으로, 보너스를 포함하지 않은 최종 점수 그래프와 동일한 모습을 볼 수 있다.
보너스를 포함한 버전에서는, ‘보너스 성공 그래프’와 ‘보너스 실패 그래프’가 서로의 봉우리를 보강하여 크게 올록볼록한 형태가 나타난 것이다. 반대로 보너스를 포함하지 않은 버전에서는, ‘보너스 성공 그래프’가 왼쪽으로 35점만큼 이동하여 봉우리끼리 상쇄된 효과가 발생했다.

용의자 2: 고정 점수 카테고리

최종 점수 그래프의 봉우리가 8개 나타난 이유는, 봉우리가 6개인 그래프 두 개가 합쳐진 결과라는 것을 확인했다. 그럼, 각 그래프가 6개 봉우리를 갖는 이유를 살펴보아야 한다. 주요인인 하단부 점수에 집중해 보자.

하단부 카테고리 중 점수가 고정된 세 가지 카테고리의 획득 여부에 따라 2×2×2=8가지 경우로 나누어 그래프를 그렸다.

• SS (Small Straight, 고정 15점)
• LS (Large Straight, 고정 30점)
• YT (Yacht, 고정 50점)

각 경우마다 봉우리가 3개씩 있고, 이 그래프들이 합쳐져서 하단부 점수의 전체 분포가 형성되었다. Small Straight 점수 획득에 실패한 경우가 매우 드물어, 나머지 4가지 경우에 해당하는 그래프가 전체 그래프 영역의 대부분을 차지한 것을 볼 수 있다.

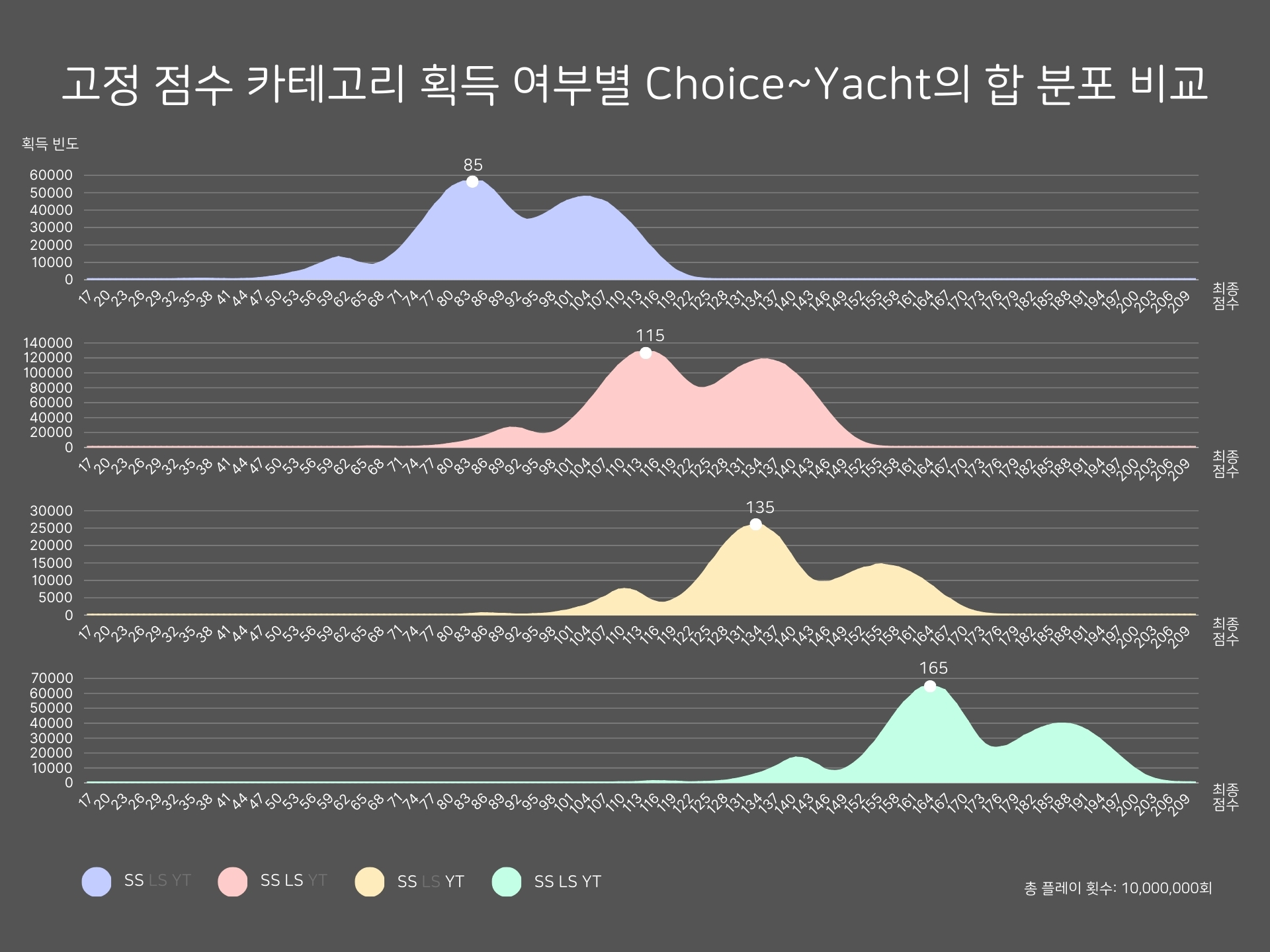
Small Straight 점수 획득에 성공한 경우 4가지만 따로 분리하여 그래프를 그려보았다. 각 그래프의 형태는 거의 동일하며, 고정 점수의 차이에 따라 X축 상에서 위치만 달라졌다는 점이 눈에 띈다.

용의자 3: 조건부 점수 카테고리

위에서 확인했듯, 봉우리가 3개 있는 그래프 8개가 합쳐져서 봉우리가 6개 있는 하단부 점수의 분포가 만들어진 것이다. 마지막으로 고정 점수 카테고리 획득 여부가 동일한 경우 내에서 봉우리 3개가 나타나는 이유를 살펴보자. 위에서 나눈 경우의 수 중 가장 횟수가 많았던 SS성공 / LS성공 / YT실패 경우를 골라 더욱 세분된 통계를 내보았다.

점수를 조건부로 획득하는 세 가지 카테고리의 획득 여부에 따라 이번에도 2×2×2=8가지 경우로 나누어 그래프를 그려보았다.

• FH (Full House)
• 3K (3 of a Kind)
• 4K (4 of a Kind)

각 경우에 해당하는 그래프에는 봉우리가 하나씩만 존재해, 더 이상 분해할 수 없는 최종 단위를 이룬다. 이 8개의 단일 봉우리가 합쳐져 3개의 봉우리가 있는 그래프 형태가 나타났다.
아까와 비슷하게 3 of a Kind 점수 획득에 실패한 경우가 매우 드물어, 나머지 4가지 경우에 해당하는 그래프가 전체 그래프 영역의 대부분을 차지한 것을 볼 수 있다.

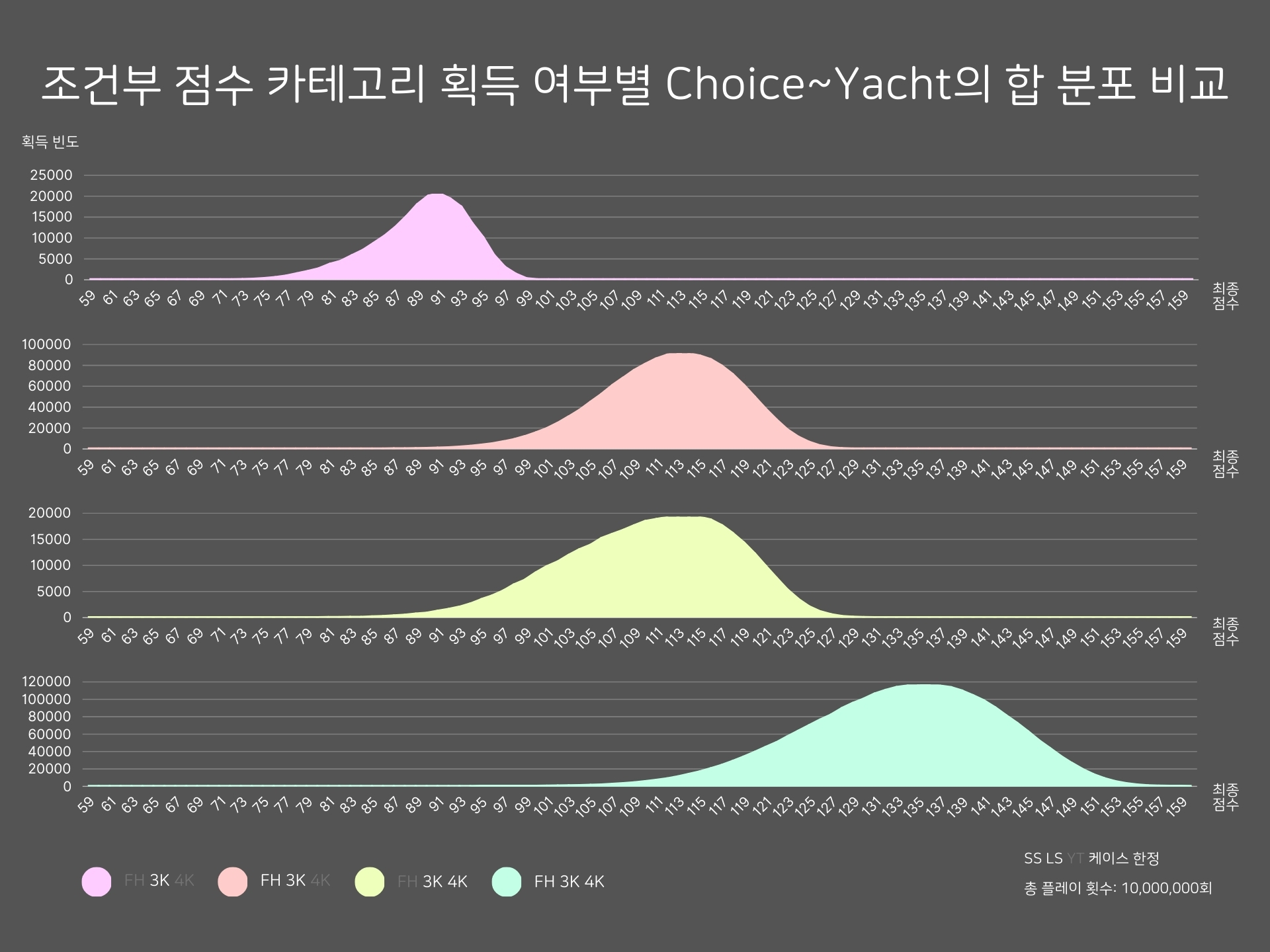
이번에도 3 of a Kind 점수 획득에 성공한 경우 4가지만 골라서 그래프를 분리하여 그려보았다. 고정 점수 카테고리 획득 여부에 따른 경우 분리와는 다르게, 각 그래프의 개형이 서로 다른 것을 볼 수 있다. 또한 포함한 성공 카테고리의 개수가 많을수록 좌우로 더 넓게 퍼진 형태를 나타낸다.
흥미로운 점은, 두 번째와 세 번째 그래프가 X축 상에서 영역을 거의 공유한다는 점이다. 이로부터 Full House와 4 of a Kind 두 카테고리에서 얻는 평균 점수가 비슷하다는 것을 추정할 수 있다. 구체적으로는 Full House의 평균 점수가 살짝 더 높을 것이다. 이는 아래에서 확인해 보겠다.

• 점수대별 카테고리 성공 여부 •

Yacht 성공 여부 분포

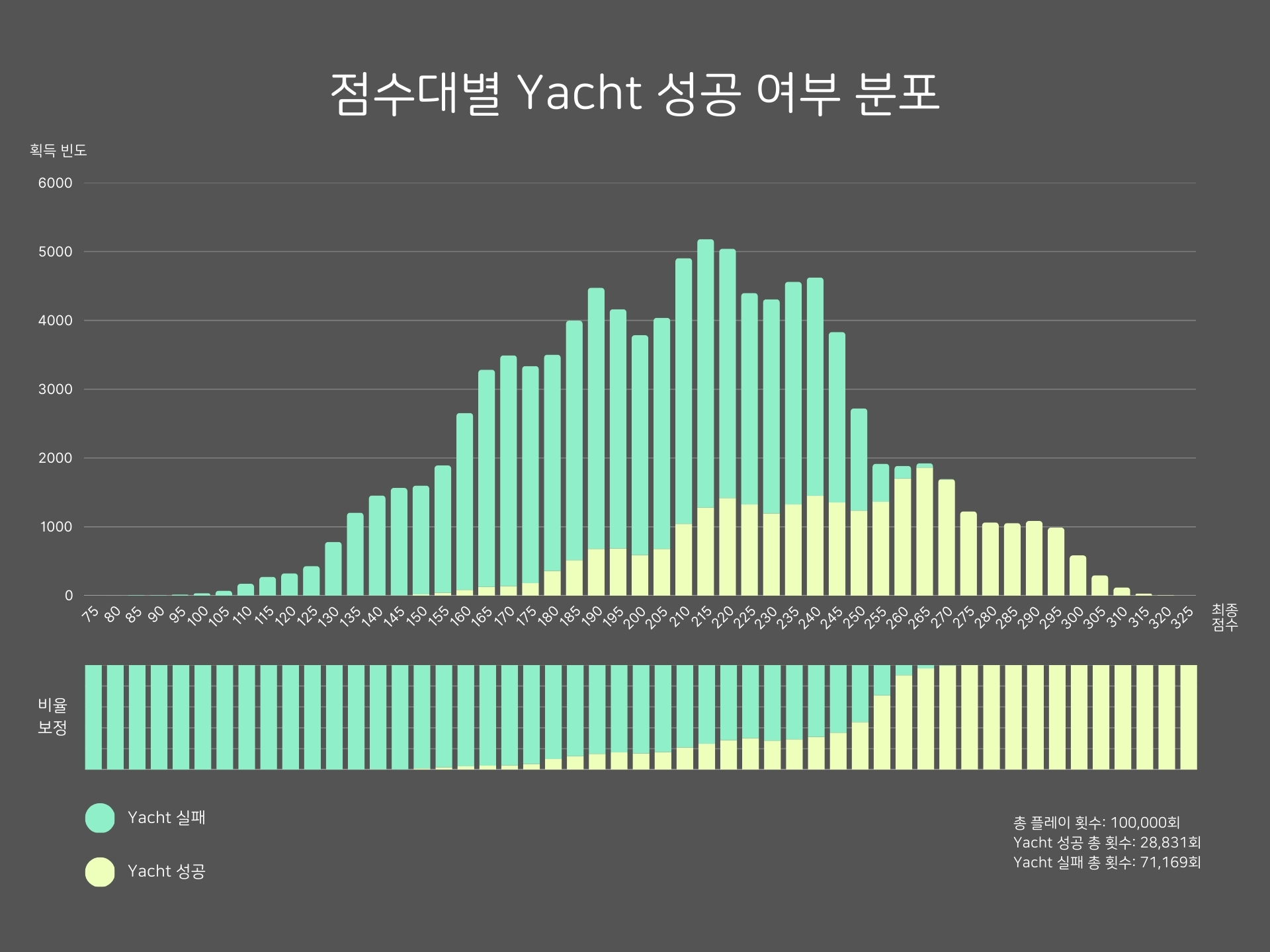
약 150점 부근부터 성공 비율이 증가하기 시작한다. 270점대 이상 구간에서는 성공 비율이 사실상 100%에 가까운 것을 볼 수 있다. 이는 270점 이상의 고득점을 위해서는 Yacht 점수 획득이 필수적이라는 해석이 가능하다.

Small Straight 성공 여부 분포

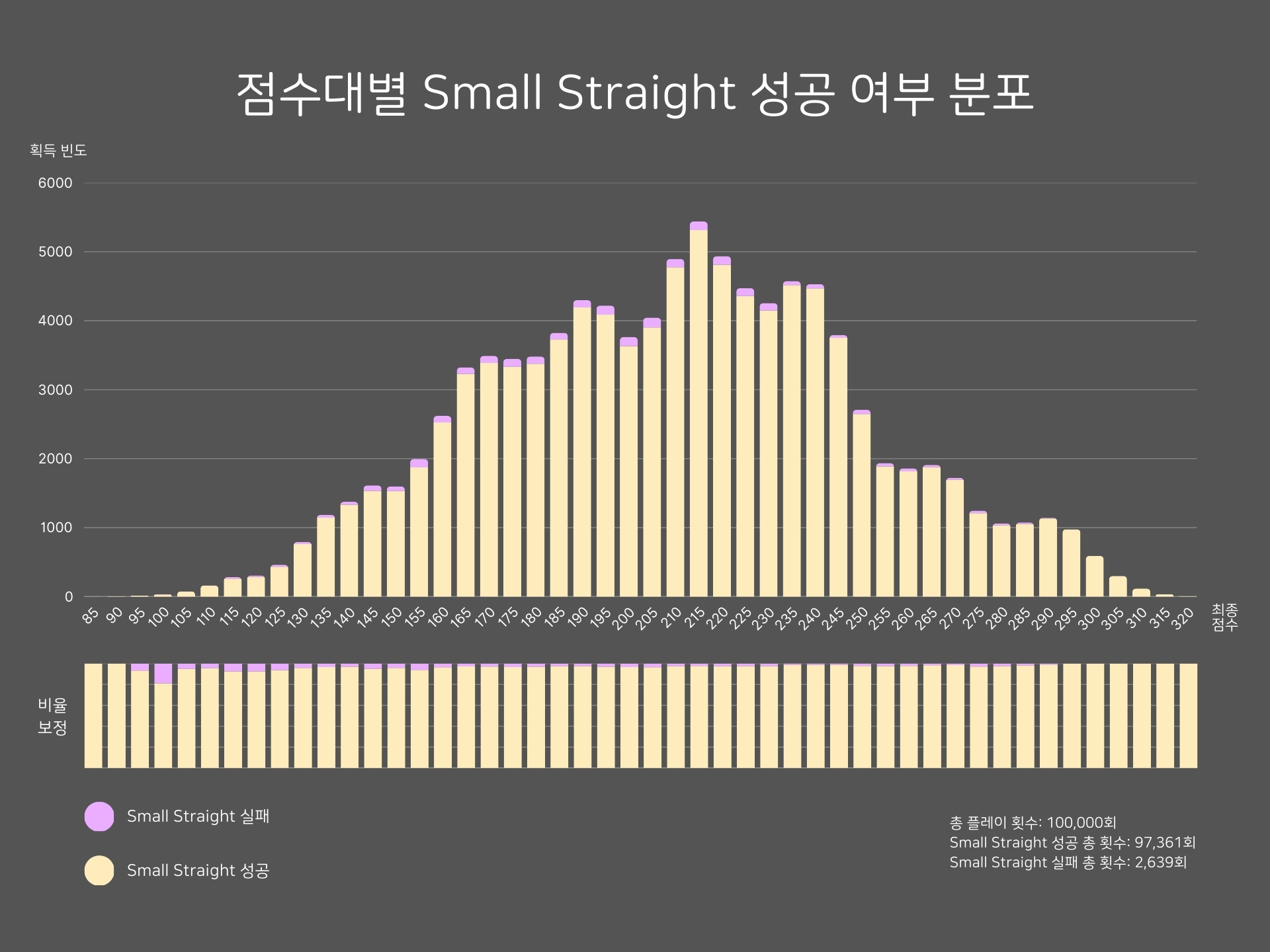
최종 점수 분포 그래프 분석에서 이미 예상했듯, 점수대 전체에 걸쳐 Small Straight 점수 획득에 실패한 비율은 매우 낮다. 100점대에서 실패 비율이 상대적으로 높은 것은, 해당 점수대 자체의 획득 빈도가 매우 낮아서 통계적 변동이 크게 반영된 결과로 추정된다.

Large Straight 성공 여부 분포

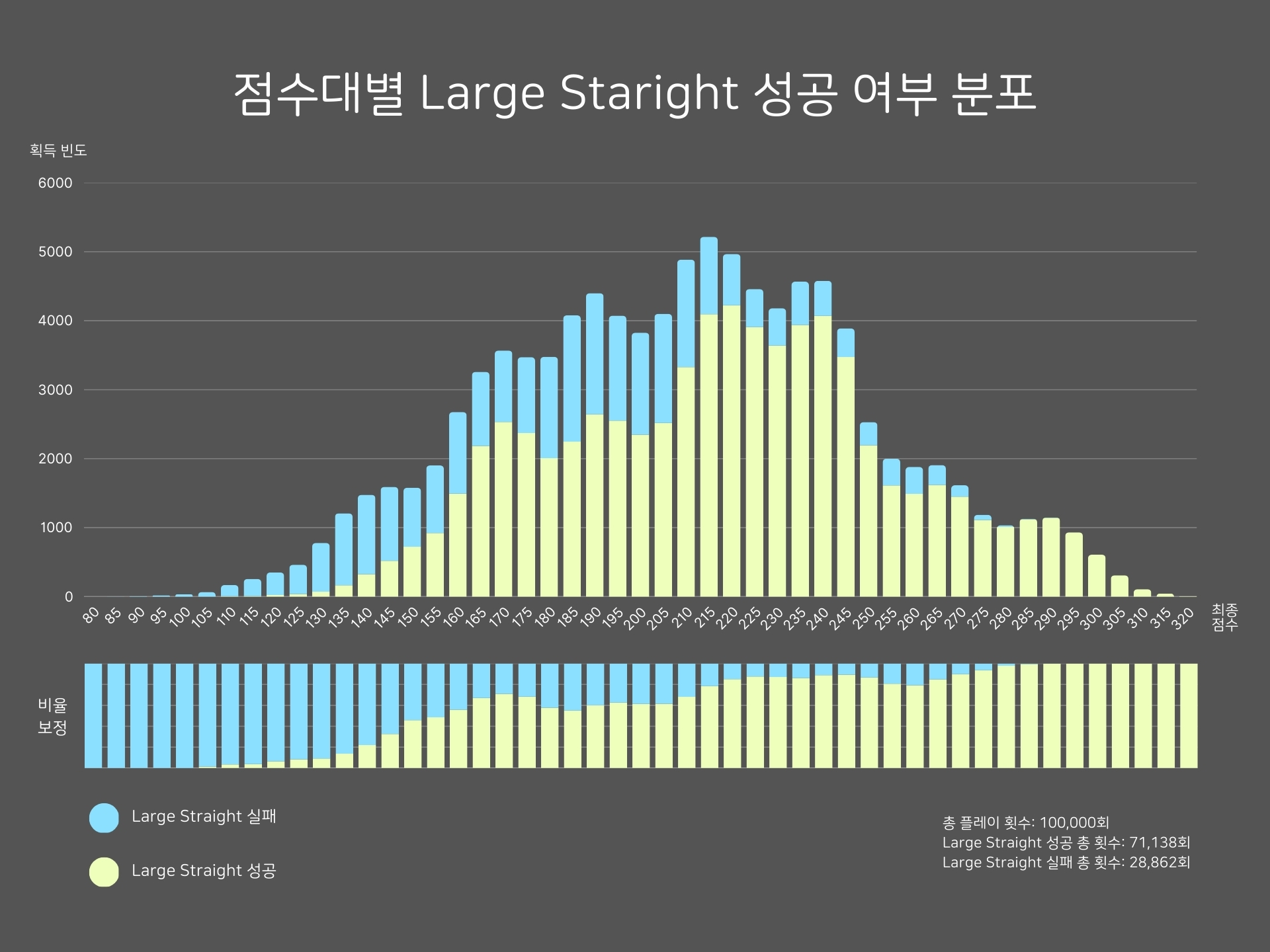
Yacht에 비하면 매우 낮은 점수대인 105점대 근처에서 성공 비율이 증가하기 시작하여, 150점대만 넘어서면 성공 비율이 절반을 넘긴다. Yacht에 비하면 전반적으로 성공할 가능성이 훨씬 높고, 최종 점수에 영향을 덜 미친다는 것을 알 수 있다. (고정 획득 점수 자체가 더 낮으므로 당연한 결과이기도 하다.)

조건부 점수 카테고리별 획득 점수 분포

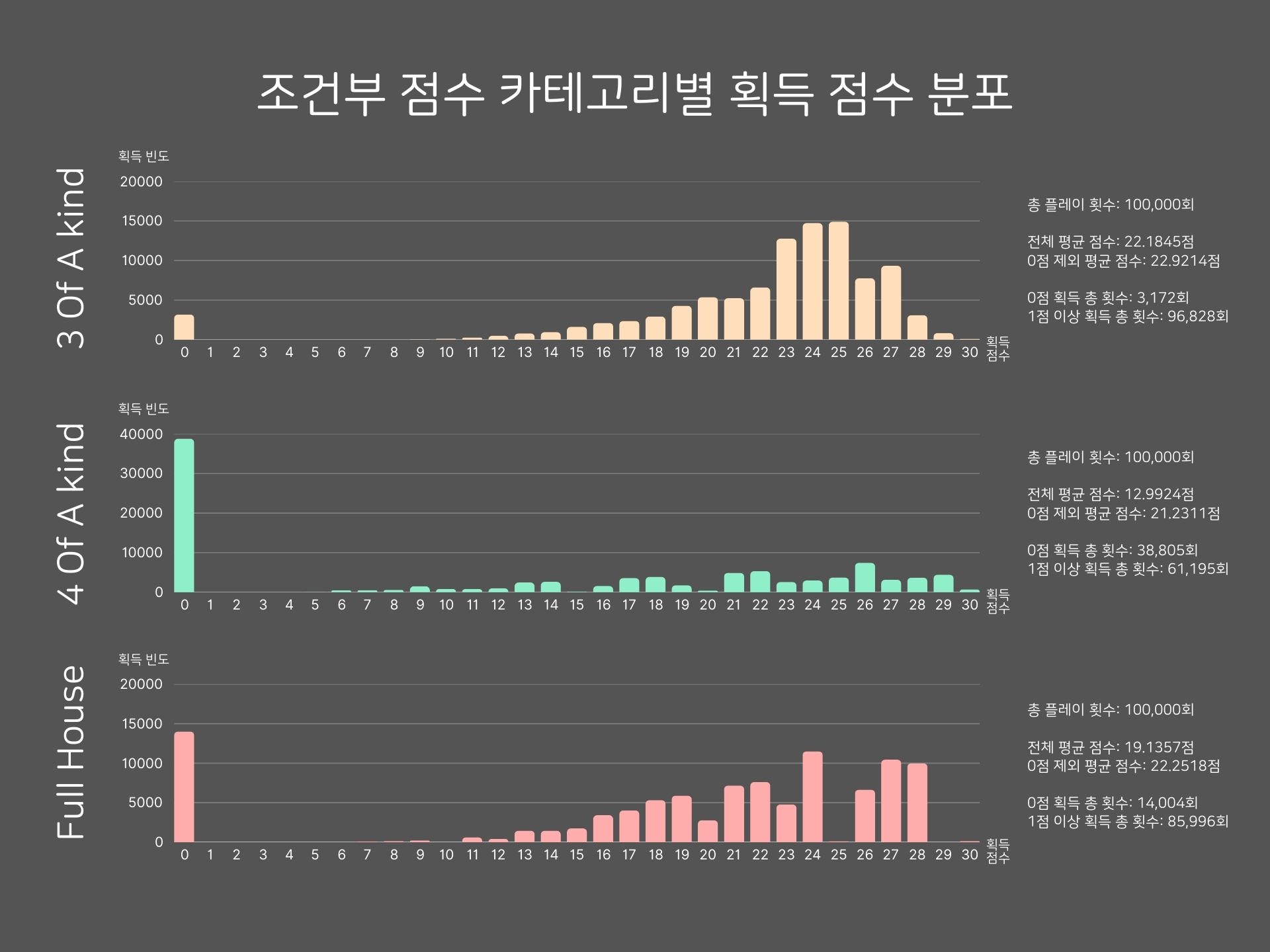
조건부로 점수를 획득하는 세 카테고리에 대해 점수 획득 분포를 살펴보았다. 먼저 3 of a Kind는 점수 획득에 실패해 0점을 기록한 빈도가 다른 두 개 카테고리에 비해 현저히 적었다.
앞서 Full House의 평균 점수가 4 of a Kind의 평균 점수보다 약간 더 높을 것으로 추정했는데, 각각 약 22점과 약 21점으로 확인되어 예측대로 들어맞았다.
4 of a Kind와 Full House 모두에서 점수가 5의 배수인 경우의 빈도가 상대적으로 낮은 편이다. 이는 주사위 5개의 눈이 모두 동일해 합이 5의 배수가 되는 경우 대부분에서 Yacht를 선택했기 때문으로 보인다. 예외적으로 4 of A Kind에서 25점을 획득한 빈도는 그리 낮지 않은데, Choice를 위해 6을 노리다가 주사위가 [6, 6, 6, 6, 1]로 나오면 Choice보다 4 of a Kind를 선택하는 것이 유리했기 때문으로 추정해볼 수 있겠다.
또한 Full House에서 29점을 획득한 빈도는 0이다. 주사위의 ‘2개의 눈이 동일하고 나머지 3개의 눈이 동일한’ Full House의 조합에서 눈의 합이 29가 나오는 경우의 수가 존재하지 않기 때문이다.

• 가중치별 점수 분포 비교 •

지난 게시글에서 상단부 점수에 가중치 3.0을 적용해 최적 선택 로직을 완성했다고 언급했다. 지금까지 살펴본 통계들은 가중치 3.0으로 시뮬레이션한 결과이다. 그러나 가중치 설정값에 따라 점수 분포가 어떻게 달라질지도 궁금했으므로, 가중치를 1.0으로 세팅한 경우의 플레이 결과와 간단히 비교해 보았다.

최종 점수 분포 비교

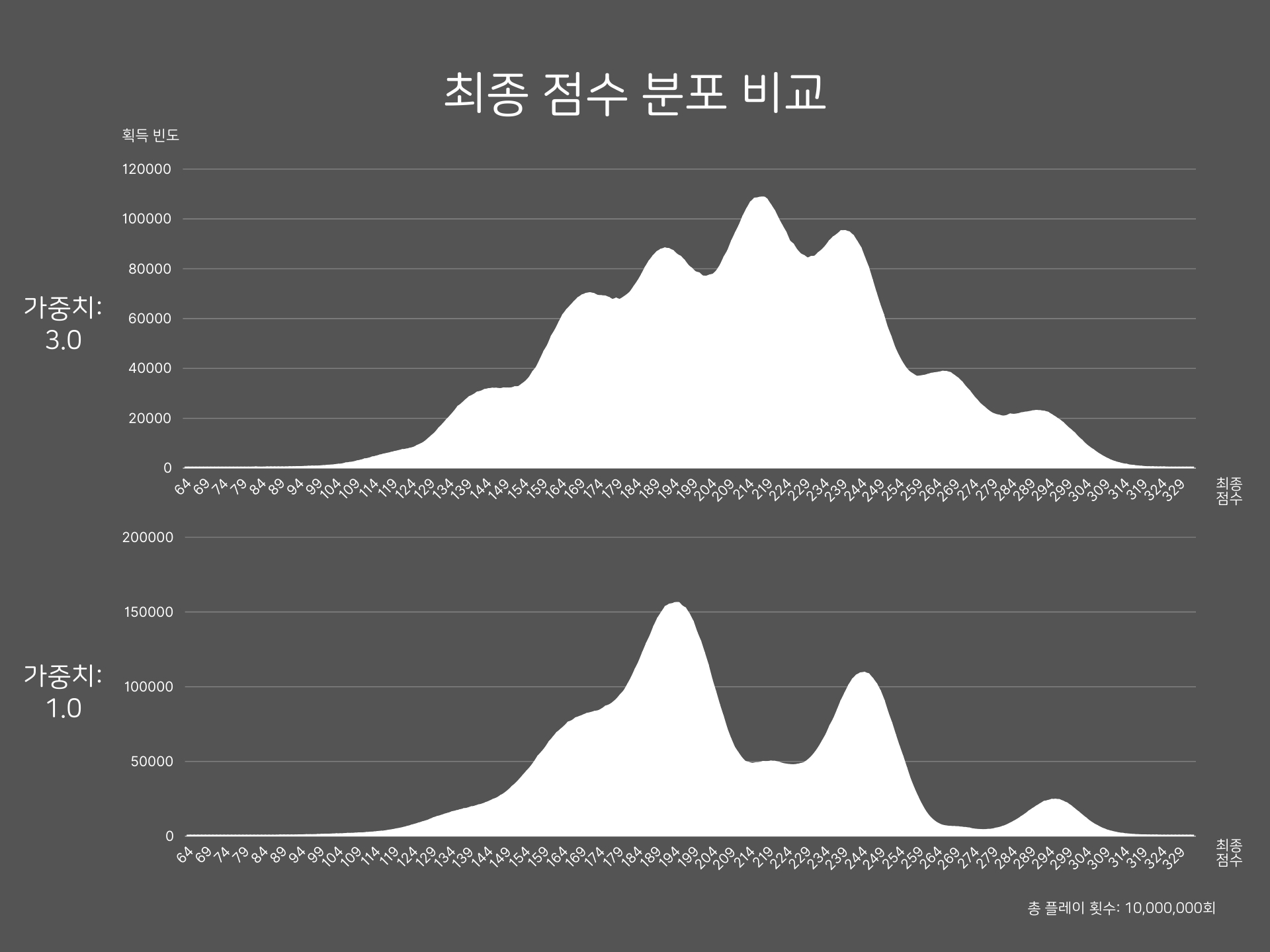
가중치가 1일 때는 봉우리의 개수뿐 아니라 전체 그래프의 형태도 크게 달라졌다. 이는 전체 분포를 세부적인 경우로 분리해 보았을 때, 각 봉우리가 겹치며 보강되거나 상쇄되는 방식이 가중치에 따라 달라졌기 때문으로 보인다.

상단부 점수 분포 비교

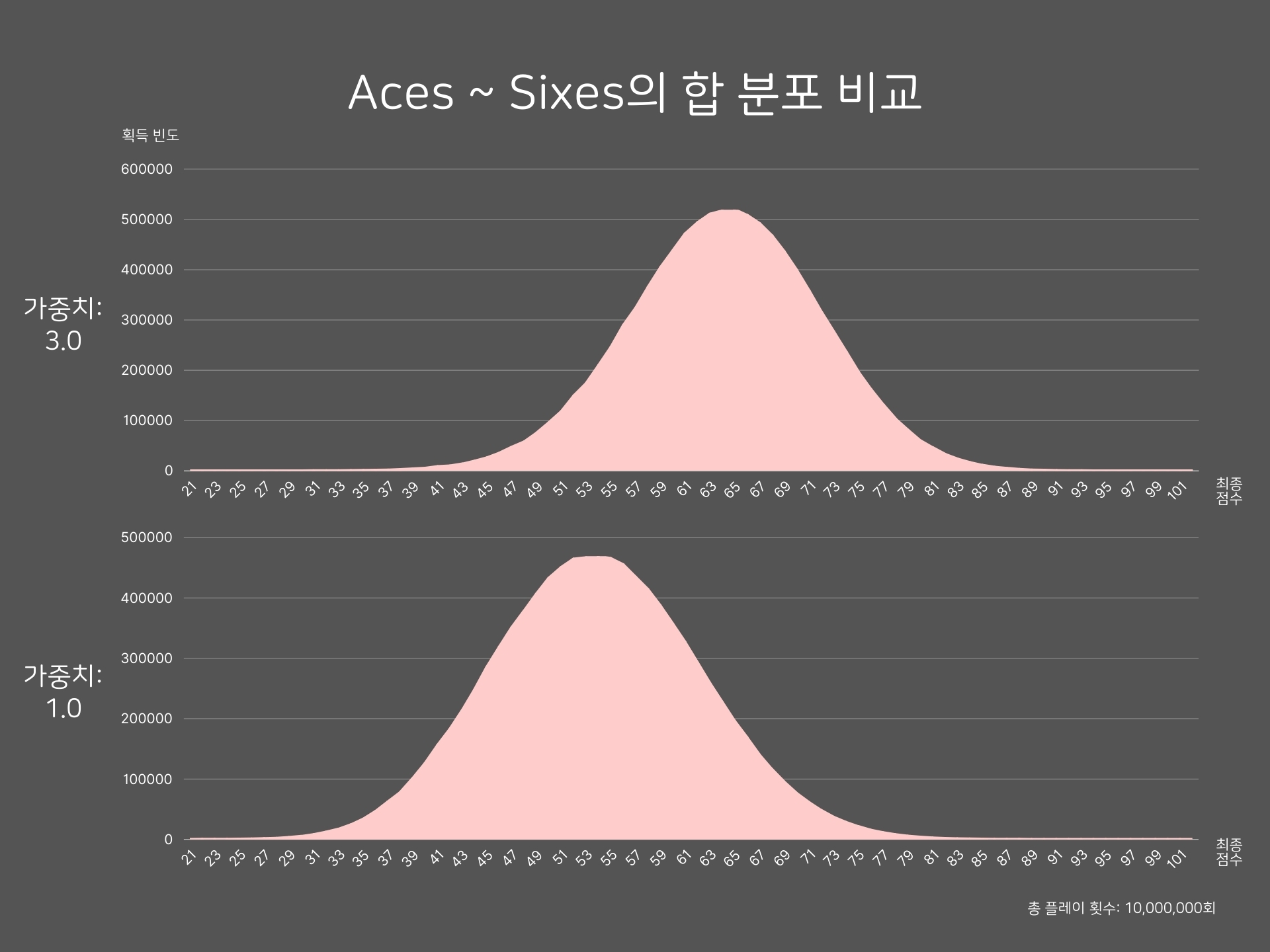
상단부 점수 분포의 형태는 여전히 정규분포와 유사한 단봉형 분포로 나타난다. 그러나 가중치가 1.0인 로직은 상단부 점수의 가치를 더 낮게 평가하므로 평균 점수가 더 낮고, 결과적으로 그래프 전체가 왼쪽으로 이동한 모습을 보인다.

하단부 점수 분포 비교

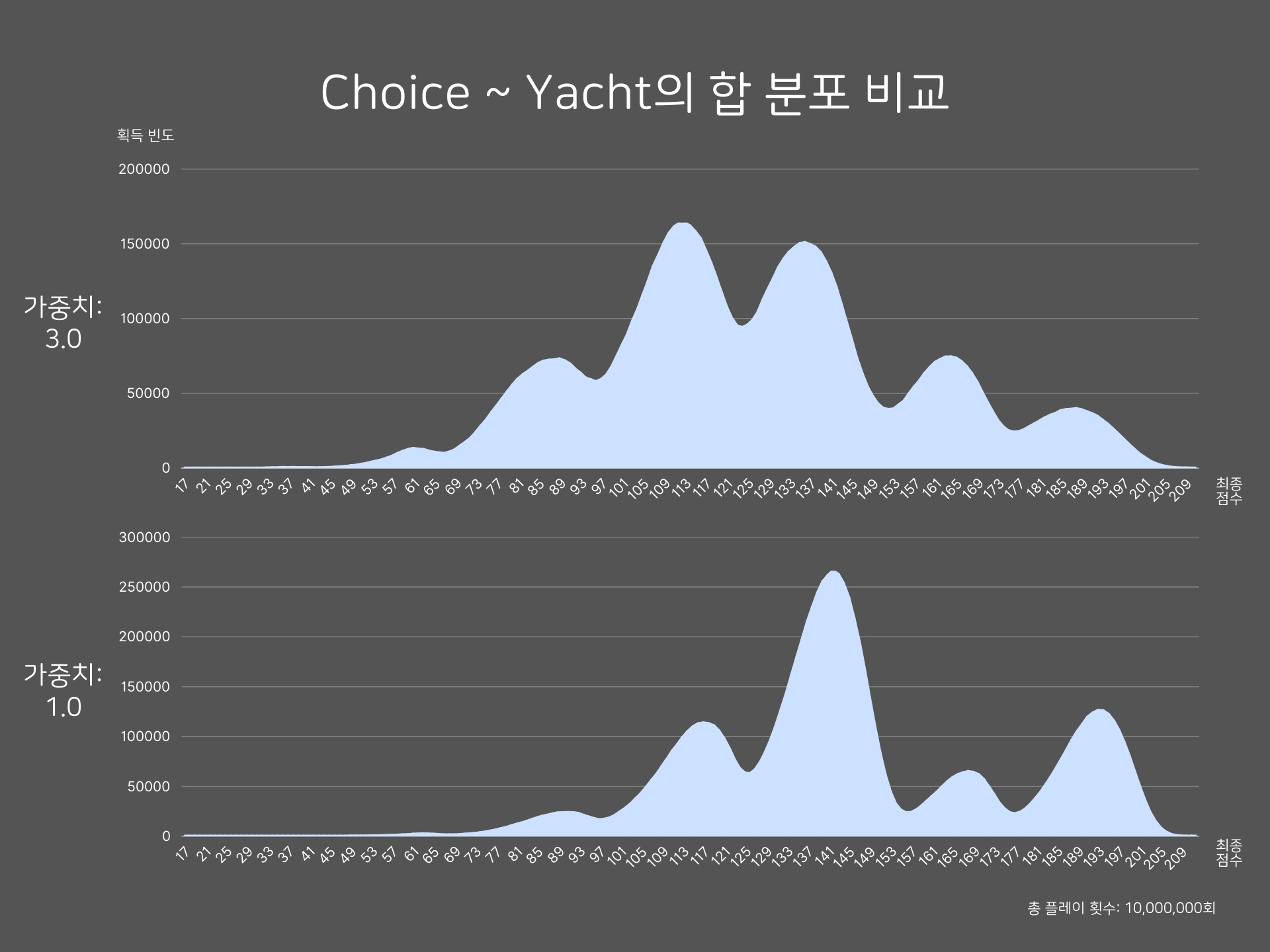
하단부에서는 가중치가 1.0일 때 봉우리가 5개로 줄었으며, 각 봉우리의 획득 빈도도 들쑥날쑥하다. 만약 가중치가 3.0인 경우와 동일하게 경우를 나눠서 그래프를 그려본다면, 봉우리 간의 보강과 상쇄가 다르게 일어나 이런 차이가 생긴다는 결론에 도달할 것이다.
우리는 가중치가 3.0으로 세팅된 로직을 사용할 예정이므로, 가중치 1.0으로 얻은 통계에 대한 분석은 여기서 마무리하겠다.